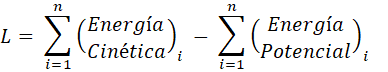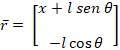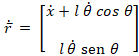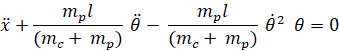Modelado del sistema carro-péndulo.

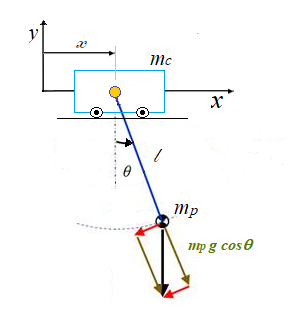
A continuación, se desarrollará el modelado del sistema carro deslizante – péndulo simple, a fin de explicar la forma en que la ecuación de Euler-Lagrange nos permite obtener las ecuaciones de movimiento del sistema mostrado en la siguiente figura:

Fig. 1. Sistema Carro – Péndulo.

La ecuación de Euler-Lagrange indica:

- (1)

Donde L, se define en general como el Lagrangiano del Sistema, y q se le conoce como el vector de coordenadas generalizadas (grados de libertad).

Así mismo, el Lagrangiano del sistema se determina restando a la energía cinética de los cuerpos rígidos que componen el sistema la energía potencial de los cuerpos rígidos que forman el sistema mecánico.

Esto es:

(2)

Donde i se refiere al cuerpo rígido i-ésimo que forma parte del sistema mecánico, y n el número total de cuerpos rígidos que conforman el sistema mecánico. Para el caso que nos ocupa, se tienen dos grados de libertad (x, θ).

Carro deslizante.

Obtengamos primero las energías del carro deslizante, para ello consideremos que la resistencia del carro al desplazarse en dirección horizontal es nula, es decir las fuerzas de fricción y la resistencia del aire al chocar con el carro son despreciables, así mismo no se consideran efectos de amortiguamiento.

Bajo estas consideraciones, la energía cinética del carro se determina como:

(3)

Por otra parte, la energía potencial del carro es cero, debido al supuesto que el carro se desplaza sobre la horizontal, y no se efectúa hundimiento del carro sobre la superficie por donde se desplaza, ni tampoco algún tipo de movimiento sobre la línea vertical.

Péndulo móvil.

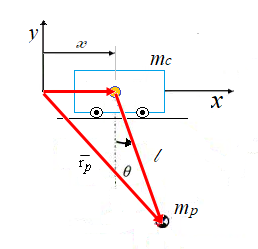
El movimiento péndulo se efectúa bajo el supuesto que no hay amortiguamientos de ningún tipo, ni tampoco pérdidas de energía por rozamiento con el aire o algún otro fenómeno que degrade el movimiento pendular. De esta forma, la energía cinética se determina a partir del vector de posición del péndulo con respecto al sistema de referencia inercial.

Fig. 2. Vector de posición del péndulo.

La posición del péndulo queda definida como:

(4)

Por lo que la velocidad queda definida como:

(5)

Por lo que la velocidad al cuadrado es:

(6)

Por lo que la energía cinética del péndulo resulta ser:

(7)

Por otra parte, la energía potencial del péndulo se determina tomando como referencia el potencial igual a cero justo en la posición en la cual el péndulo se encuentra alineado sobre el eje vertical. En esta posición, el péndulo adopta la posición más baja que puede lograr. Por lo que la energía potencial se determina por la ecuación:

(8)

Sustituyendo (3), (7) y (8) en la ecuación de Lagrange (2), resulta:

(9)

Aplicando la ecuación Lagrangiana para la coordenada generalizada x, tenemos:

(10)

Por lo que,

(11)

Así mismo, resulta que:

(12)

Por lo que la ecuación de movimiento para la coordenada x queda definida como:

(13)

Si consideramos que la oscilación del péndulo se efectúa sobre ángulos pequeños, resulta que esta ecuación se puede simplificar, dado que θ ≈ sen θ y que cos θ ≈ 1, por lo que la ecuación de movimiento se reduce a:

(14)

Tomando como factor común la aceleración lineal:

(15)

Dividiendo entre la suma de las masas, resulta:

(16)

Calculando ahora la ecuación de movimiento para la coordenada generalizada θ, resulta:

(17)

Por lo que,

(18)

Así mismo,

(19)

Sustituyendo (18) y (19) en (1), tenemos:

+ (20)

Considerando nuevamente que la oscilación del péndulo se efectúa sobre ángulos pequeños, resulta que esta ecuación se puede simplificar, dado que θ ≈ sen θ y que cos θ ≈ 1, obteniendo:

(21)

Dividiendo entre m_p l , resulta:

(22)

Las ecuaciones (16) y (22) resultan ser ecuaciones diferenciales ordinarias de segundo orden, las cuales se encuentran acopladas, esto es que se deben resolver simultáneamente dadas las restricciones de movimiento del sistema carro-péndulo.

Despejando de (22) la aceleración lineal, y sustituyendo en (16), y simplificando resulta:

(23)

La solución de esta ecuación se puede realizar aplicando métodos numéricos con base en condiciones iniciales de velocidad y aceleración iguales a cero, y un ángulo inicial pequeño. Queda para el lector la tarea de seleccionar el método numérico adecuado para resolver la ecuación de movimiento.

Así mismo, se puede reconocer de ésta última ecuación que, si la masa del carro es considerablemente mayor a la masa del péndulo el comportamiento de la oscilación del péndulo sería similar a la oscilación del péndulo simple. Adicionalmente, dado que para ángulos

Al desarrollar la ecuación (23) con base en una oscilación periódica cíclica, resulta bajo el supuesto que:

(24)

Al derivar:

(25)

Por lo que

(26)

Analizando esta última función para un valor de ángulo inicial de 30[°, es válido considerar que la ecuación (26) presenta valores cercanos a cero, queda como ejercicio para el lector comprobar dicha afirmación. Por lo que la velocidad angular aproximada resulta ser:

(27)

Por otra parte, al determinar la tensión de la cuerda del péndulo, y proyectando dicha fuerza sobre el eje horizontal resulta:

(28)

De la segunda ley de Newton, la fuerza que mueve el carro es:

(29)

Igualando (28) y (29) y despejando la aceleración lineal, resulta:

(30)

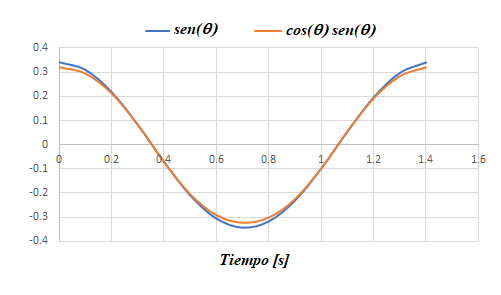
Al graficar la función cos θ senθ, en un ciclo de la función senθ se observa:

Gráfica 1. Similitud del periodo de senθ y cosθsenθ.

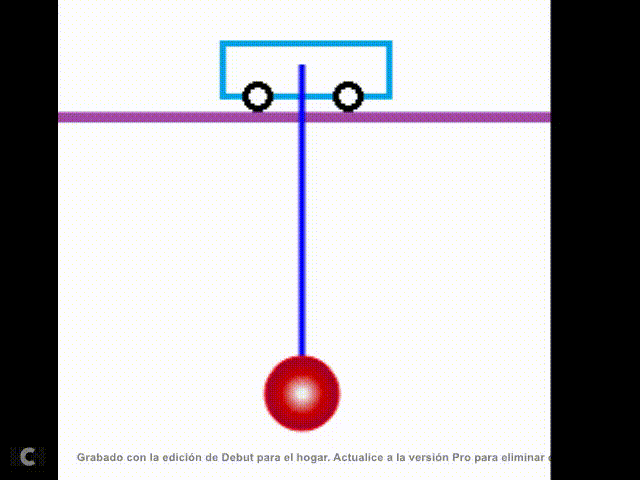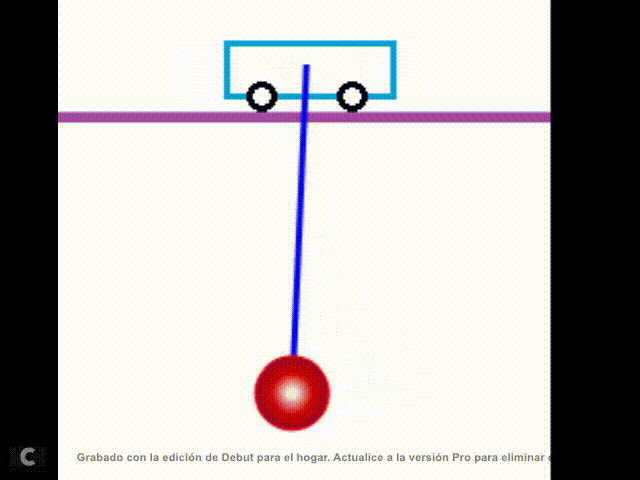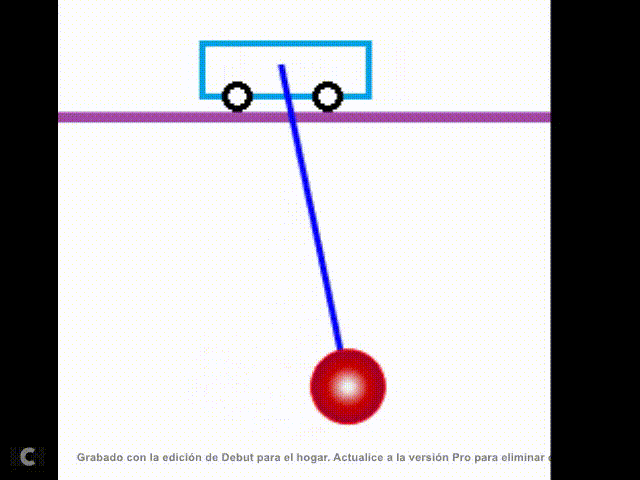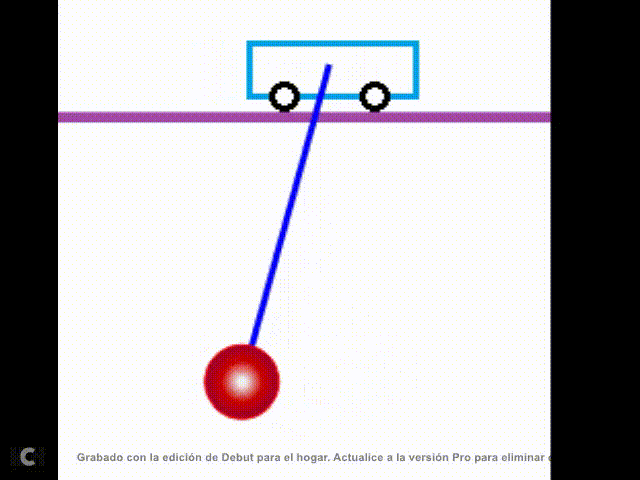
Por lo que puede deducirse que tanto x, como θ son funciones periódicas, y ambas tiene la misma velocidad angular (w). Al resolver las ecuaciones (16) y (22) con la aproximación (27), se obtuvo mediante simulación el movimiento del sistema: