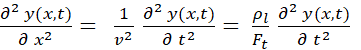Ecuación de onda y principio de superposición.

En general, la ecuación de una onda plana que se propaga en dirección x esta dada por la siguiente igualdad:

(1)

Siendo v la velocidad de la onda, la densidad lineal de la cuerda y la fuerza de tensión de la cuerda. Una de sus propiedades, es la linealidad. Esto es, que se cumple el principio de superposición.

Consideremos y₁(x, t) y y₂(x, t) dos ondas viajeras que satisfacen la ecuación 1. Entonces su suma también satisface la ecuación 1, esto es:

(2)

Superposición de ondas por pulso.

Por lo regular, la superposición de ondas que presentan un tipo de pulso suele realizarse cuando las ondas se desplazan a diferentes velocidades, independientemente si la dirección coindice o no. La forma que adopta la superposición de las ondas depende del perfil de cada onda, generando así una variación del perfil durante el tiempo que coinciden mayoritariamente ambos perfiles, para finalmente estabilizar el perfil resultante mostrando nulo efecto de superposición.

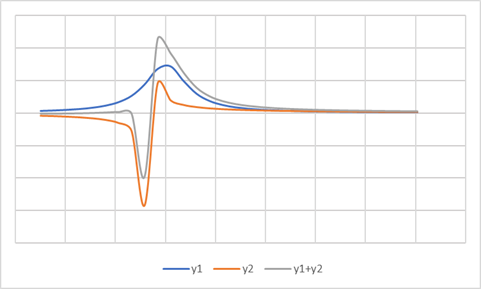
Fig.1 Superposición de ondas por impulso

La Fig.1 presenta la superposición de dos ondas por impulso con diferente forma, en el instante que se presenta las suma ( y₁ + y₂ ) muestra gráficamente el perfil obtenido. Dado que las velocidades de las funciones son diferentes, la suma se estabiliza en estado permanente.

Superposición de ondas sinusoidales.

El principio de superposición de ondas aplica de diversas maneras, ya sea en la superposición de luces, así como en la superposición de sonidos. En ejemplo típico es el ambiente que presenta una discoteca en donde luces y sonido se combinan para lograr efectos propios del ambiente.

Fig.1 Superposición de ondas de luz en una discoteca [1].

De esta forma, no importa si se superponen 2, 3, 10 o una cantidad mayor de ondas simples. El principio de superposición aplica logrando fenómenos realmente interesantes.

Por otra parte, vale la pena recordar que el matemático Augustin Jean Fourier, de origen francés demostró a través de la Serie que lleva su apellido (Serie de Fourier) que cualquier oscilación periódica puede generarse mediante la superposición de ondas periódicas simples.

Dada la diversa cantidad de formas y variaciones que puede presentar la suma de dos funciones de ondas viajeras de tipo sinusoidal:

(3)

(4)

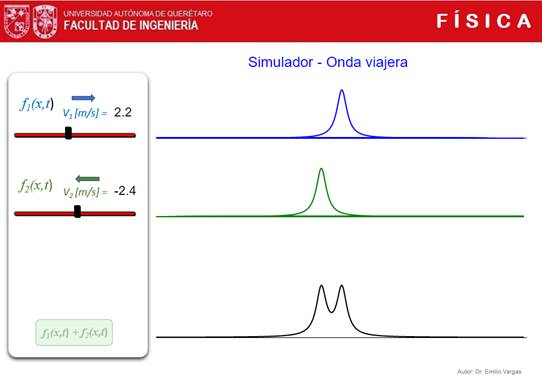
Herramienta didáctica. Superposición de ondas.

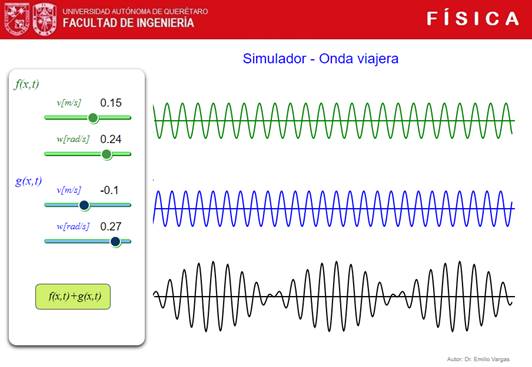
Se recomienda utilizar los simuladores de superposición de ondas viajeras, a fin de que el estudiante reconozca algunas de las formas típicas que presenta la superposición de ondas, como: a) Ondas que presentan la misma amplitud, b) ondas que presentan diferente velocidad en el mismo sentido, c) ondas que presentan la misma amplitud, velocidad diferente y sentido diferente, d) ondas que presentan diferente frecuencia, etc.

Fig. 2 Simulador de Superposición de ondas viajeras simples.

Fig. 3 Simulador de Superposición de ondas viajeras senoidales.

Referencias.

[1] pinteres.com, sitio en internet: https://www.pinterest.com.mx/pin/459367230721458128/ , consulta: 25/03/2022.