|
Péndulo simple. |
|
|
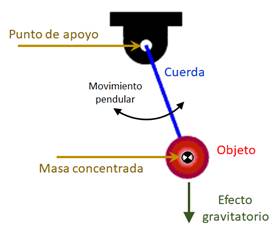
Péndulo simple. Definición. El péndulo simple es una
idealización que consiste en considerar que en un punto de apoyo se coloca el
extremo de una cuerda inextensible de masa despreciable, en el otro extremo
de la cuerda se ubica un objeto de masa m, de forma que al orientar la cuerda
en una dirección fuera de la vertical y al soltar el objeto se produce un
movimiento pendular tipo vaivén ocasionado por el efecto gravitatorio. |
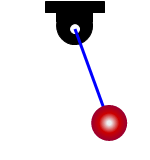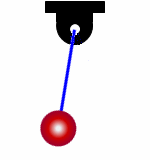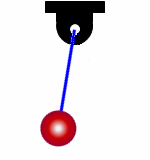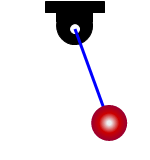
Fig. 1 Elementos del péndulo simple. |
|
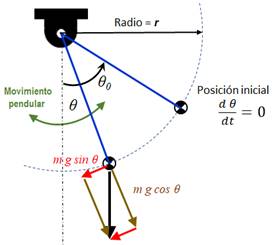
Fig.2 Movimiento pendular tipo vaivén. |
|
|
Análisis
energético.
Fig.3 Parámetros del péndulo simple. |
Consideraciones: · La masa del
objeto se concentra en un punto (centro de gravedad). · El objeto se
considera una partícula. · No hay
pérdidas energéticas. · El centro de
gravedad describe una trayectoria circular. Bajo estas consideraciones es posible plantear la
ecuación de equilibrio energético con base en el
principio de conservación de energía. |
|
Energía
cinética (Ec). Es la
energía mecánica derivada del movimiento de la partícula, tomando como base
la velocidad lineal de la partícula (v), considerando que la cuerda tiene una
longitud r, su
ecuación fundamental es:
Energía
potencia (Ep). Es la energía mecánica derivada por la altura potencial
de un objeto, ocasionada por el efecto gravitatorio. Para el caso del péndulo
simple, se considera la altura medida con respecto al punto más bajo de la
partícula (posición vertical de la cuerda). |
|
|
La
ecuación fundamental de la energía potencial resulta ser:
Donde:
m - es
la masa de la partícula [kg]. r - la
longitud de la cuerda [m]. θ - el
ángulo del péndulo con respecto a la vertical [rad]. |
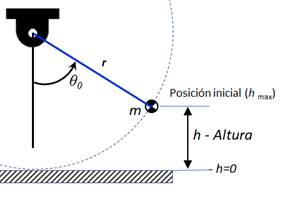
Fig. 4 Altura potencial del péndulo. |
|
De
esta forma, la energía total (Et) del movimiento pendular está dada por la
expresión:
|
|
|
Derivando esta expresión y simplificando
se obtiene:
La
solución de esta ecuación diferencial no lineal de segundo orden no se puede
resolver en términos de funciones elementales. Una solución aproximada se
obtiene considerando ángulos pequeños, de forma que se linealiza la ecuación
asumiendo la aproximación θ ≈ seno θ. De esta forma, la
solución de la ecuación (4) resulta ser:
Siendo su velocidad angular: y su periodo:
Que corresponde a un Movimiento Armónico Simple. |
|
|
|
|
|
|
|
|