Fenómenos de movimiento ondulatorio. Péndulos simple y compuesto.
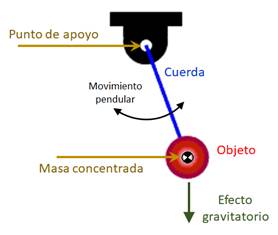
Péndulo simple. Definición. El péndulo simple es una idealización que consiste en considerar que en un punto de apoyo se coloca el extremo de una cuerda inextensible de masa despreciable, en el otro extremo de la cuerda se ubica un objeto de masa m, de forma que al orientar la cuerda en una dirección fuera de la vertical y al soltar el objeto se produce un movimiento pendular tipo vaivén ocasionado por el efecto gravitatorio.	Fig. 1 Elementos del péndulo simple.
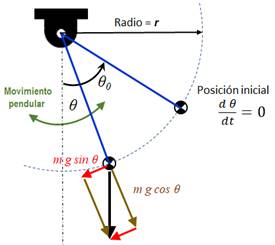
Fig.2 Movimiento pendular tipo vaivén.

Análisis energético. Fig.3 Parámetros del péndulo simple.

Consideraciones: · La masa del objeto se concentra en un punto (centro de gravedad). · El objeto se considera una partícula. · No hay pérdidas energéticas. · El centro de gravedad describe una trayectoria circular. Bajo estas consideraciones es posible plantear la ecuación de equilibrio energético con base en el principio de conservación de energía.

Energía cinética (Ec). Es la energía mecánica derivada del movimiento de la partícula, tomando como base la velocidad lineal de la partícula (v), considerando que la cuerda tiene una longitud r, su ecuación fundamental es: (1) Energía potencia (Ep). Es la energía mecánica derivada por la altura potencial de un objeto, ocasionada por el efecto gravitatorio. Para el caso del péndulo simple, se considera la altura medida con respecto al punto más bajo de la partícula (posición vertical de la cuerda).
La ecuación fundamental de la energía potencial resulta ser: (2) Donde: m - es la masa de la partícula [kg]. r - la longitud de la cuerda [m]. θ - el ángulo del péndulo con respecto a la vertical [rad].	Fig. 4 Altura potencial del péndulo.
De esta forma, la energía total (Et) del movimiento pendular está dada por la expresión: (3)
Derivando esta expresión y simplificando se obtiene: (4) La solución de esta ecuación diferencial no lineal de segundo orden no se puede resolver en términos de funciones elementales. Una solución aproximada se obtiene considerando ángulos pequeños, de forma que se linealiza la ecuación asumiendo la aproximación θ ≈ seno θ. De esta forma, la solución de la ecuación (4) resulta ser: (5) Siendo su velocidad angular: (6) y su periodo: (7) Que corresponde a un Movimiento Armónico Simple.
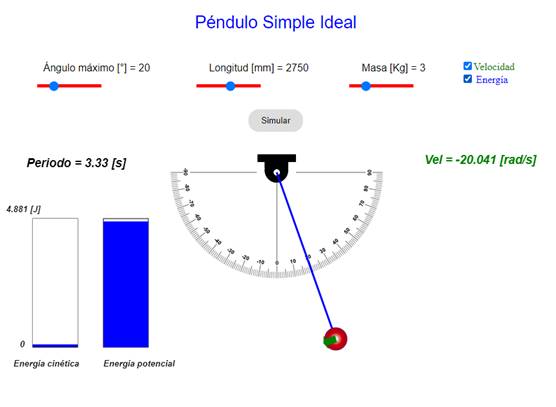
Herramienta didáctica. Fig. 5 Interfaz del simulador de péndulo simple.

Péndulo compuesto.

Definición.

El péndulo compuesto es una idealización que consiste en considerar uno o varios cuerpos rígidos unidos de forma permanente, de forma que el giro del cuerpo rígido se produce por efecto de la gravedad cuando el centro de gravedad del cuerpo rígido se encuentra orientado en un ángulo diferente a la vertical y el cuerpo rígido se suelta, propiciando el movimiento pendular.

.

Fig. 6 Elementos de un péndulo compuesto.

Para generar el modelo que describa el movimiento del péndulo compuesto, primero se efectuará la parametrización de las variables que nos permitirán definir las ecuaciones deseadas. Considerando la siguiente figura:

Fig. 7 Parámetros del péndulo compuesto.

Donde:	Dp	Es la distancia del extremo superior de placa al eje de giro (Pivote) [m].
	Lp	Es el largo de la placa [m].
	Ap	Es el ancho de la placa [m].
	r	Es el radio del disco [m].
	Xd	Es la distancia del eje de giro al centro de gravedad del disco [m].
	Xp	Es la distancia del eje de giro al centro de gravedad de la placa [m].
	Xpc	Es la distancia del eje de giro al centro de gravedad del péndulo [m].
	Θ0	Es el ángulo máximo del péndulo [rad].

Análisis energético. Fig.8 Movimiento pendular.

Consideraciones: · La masa del péndulo se ubica en un punto (centro de gravedad). · El péndulo se considera un cuerpo rígido. · El péndulo tiene una inercia (Ipc). · No hay pérdidas energéticas. · El centro de gravedad describe una trayectoria circular. Bajo estas consideraciones es posible plantear la ecuación de equilibrio energético con base en el principio de conservación de energía.

Energía cinética. En general la energía cinética de un cuerpo rígido se define como: (8) Siendo v la velocidad lineal del centro de gravedad de péndulo, w la velocidad angular. En el caso del péndulo éste efectúa movimiento de rotación pura por lo que la ecuación anterior toma la forma: (9) Por lo que es necesario obtener Xpc, así como de Ipc. Para ello, se procederá a determinar la distancia y posteriormente la inercia. (10) Siendo mp la masa de la placa [kg] y md la nada del disco [kg]. Para obtener la Inercia de la placa con respecto al eje de giro, primero se calcula la inercia de la placa con respecto a su centro de gravedad y posteriormente se traslada dicha inercia al eje de giro, aplicando el principio de los ejes paralelos o “Teorema de Steiner”. De acuerdo a las tablas de inercia, resulta: (11) De forma análoga, la inercia del disco con respecto al eje de giro es: (12) Por lo que la suma de (11) y (12) nos permite obtener la inercia total, que representa la inercia del péndulo compuesto. (13) Por lo que la energía cinética se expresa como: (14)
Energía potencial. La ecuación fundamental de la energía potencial resulta ser: (15) Siendo mpc = mp + md , la masa del péndulo compuesto [kg.].	Fig. 9 Movimiento pendular.
Bajo estas consideraciones, con base en el principio de conservación de energía , al sumar ambas energías, derivando y simplificando se obtiene: (16) Una solución aproximada se obtiene considerando ángulos pequeños, de forma que se linealiza la ecuación asumiendo la aproximación θ ≈ seno θ. De esta forma, la solución de la ecuación (16) resulta ser: (17) Siendo su velocidad angular: (18) Y su periodo: (19) Que corresponde a un Movimiento Armónico Simple.
Herramienta didáctica Fig. 10 Interfaz del Simulador de un péndulo compuesto. Bibliografía: [1] Universidad del País Vasco, Oscilaciones, Péndulo Compuesto: Sitio en internet: http://www.sc.ehu.es/sbweb/fisica3/oscilaciones/compuesto/compuesto.html , consulta: 04/02/2022. [2] Fisica Recretiva, https://www.fisicarecreativa.com/guias/pendulo2.pdf consulta: 10/02/2022.